플로이드의 토끼와 거북이 알고리즘(사이클 탐지 알고리즘)

개요#

토끼와 거북이 알고리즘, Floyd’s Tortoise and Hare Algorithm은 연결 리스트에서 사이클의 존재 여부를 찾기 위해 고안된 알고리즘입니다.

이 알고리즘은 1967년 Robert W. Floyd의 논문에 나타났으며, “Tortoise and Hare”라는 이름은 이솝 우화에서 유래했습니다.

또한 이 알고리즘을 활용하면 사이클의 시작점과 길이를 찾을 수 있습니다.

판별하는데 필요한 시간복잡도는 $O(\mu + \lambda)$ (시작점부터 사이클 시작점까지 거리: $\mu$ , 사이클 길이: $\lambda$ ) 이며 필요한 공간복잡도는 $O(1)$ 입니다.

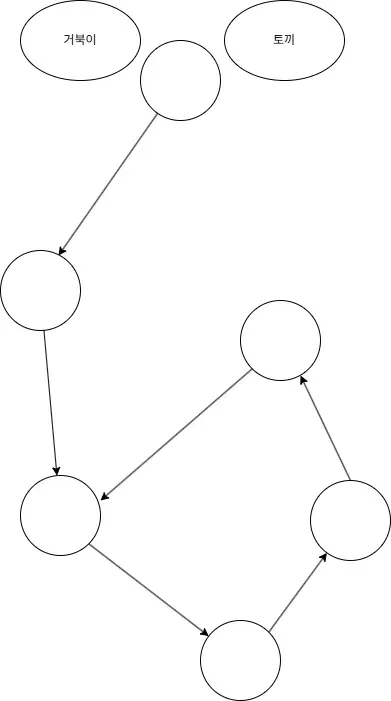
먼저 토끼라고 이름을 붙인 포인터와 거북이라고 이름을 붙인 포인터를 시작점에 둡니다.

과정1 과정2

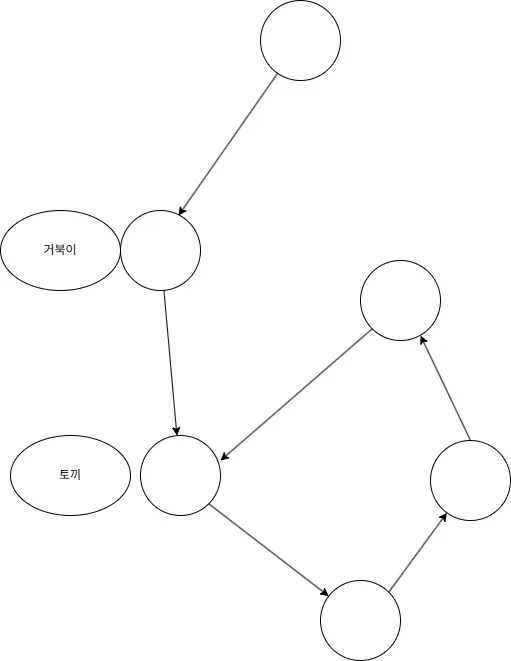
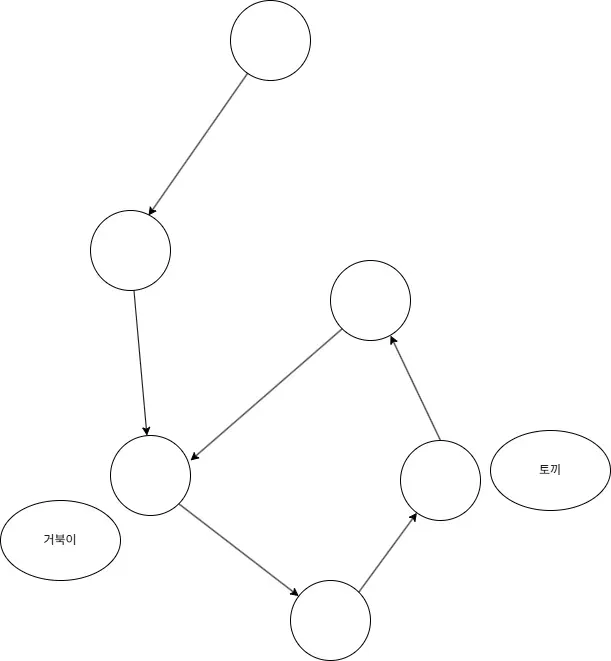
토끼 포인터는 한 번 움직일 때 2칸씩 이동하고 거북이 포인터는 한 번 움직일 때 1칸씩 이동합니다.

과정3

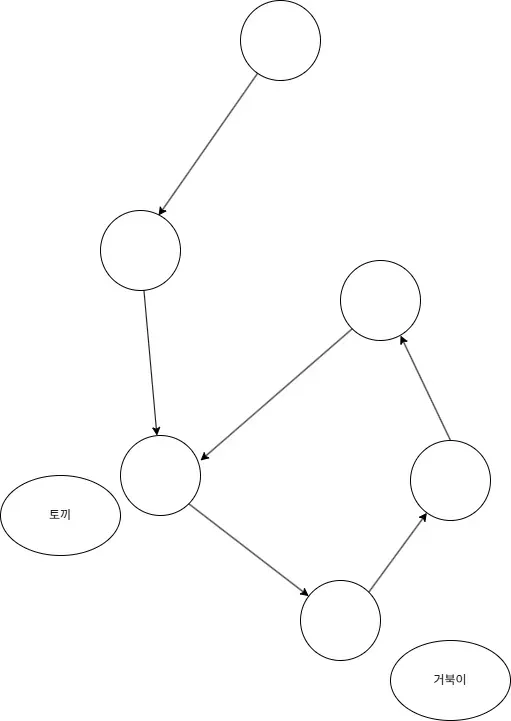
두 포인터를 동시에 이동시키면서 만약 두 포인터가 만나면 사이클이 존재하는 것이고 토끼 포인터가 리스트의 끝에 도달한다면 연결 리스트에 사이클이 없는 것입니다.

리제로

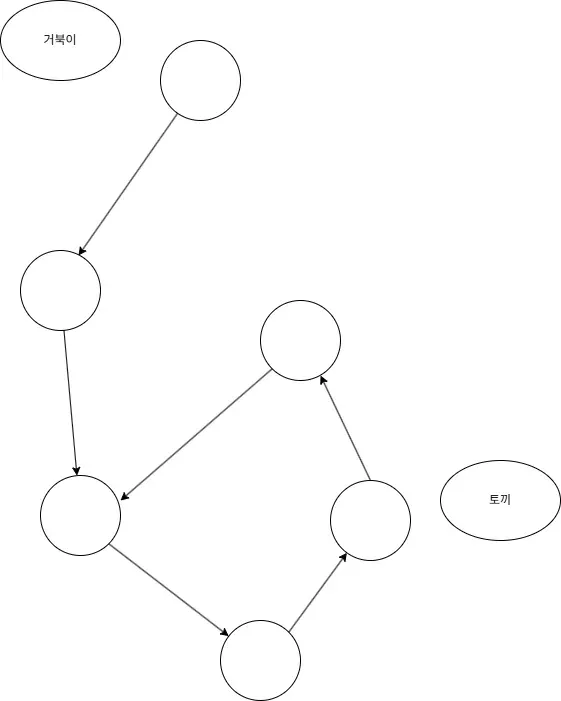
사이클의 시작점을 찾으려면 만난 후에 거북이를 시작점으로 다시 옮깁니다.

다시 과정

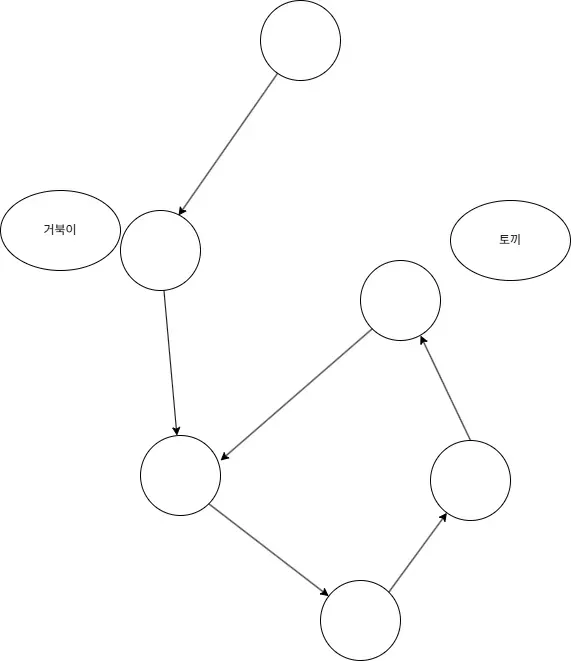
그 후 이번엔 두 포인터를 한 칸 씩 이동시킵니다.

시작점

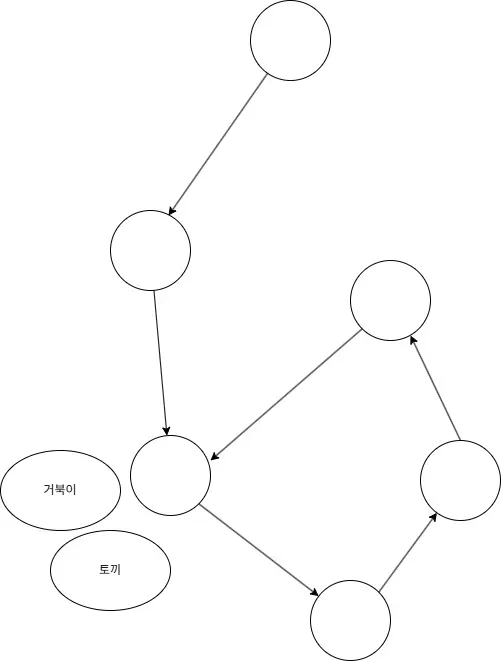
그러면 두 포인터가 만나는 지점이 사이클의 시작점입니다.

첫 만남까지 거북이가 이동한 거리는 다음과 같습니다.

$\mu + m$

토끼가 이동한 거리는 거북이보다 2배 속도가 빠르므로 다음과 같이 됩니다.

$2i=2(\mu+m)$

다시 토끼가 이동한 거리를 써보면 토끼는 시작점 -> 사이클 회전 -> m만큼 추가 이동이므로 아래와 같이 됩니다.

$2i = \mu + k\lambda + m$

즉 정리하면 다음과 같습니다.

$2(\mu + m)=\mu+k\lambda+m$

$\mu+m=k\lambda$

그러면 처음 만나는 위치는 사이클의 시작지점에서 $m$ 만큼 떨어진 지점에서 만납니다.

사이클의 시작지점은 거북이의 경우 $\mu$ 칸, 토끼의 경우 $k\lambda$ 칸 이동하면 찾을 수 있습니다.

추가적으로 $m$ 은 사이클의 시작지점에서 거리이므로 아래의 식이 성립합니다.

$(k\lambda - \mu) \mod \lambda$

따라서 사이클 시작점에서 처음 만나는 지점까지의 거리의 식이 유도됩니다.

$\lambda - (\mu \mod \lambda)$