두 선분이 있을 때 교점의 좌표를 구하는 알고리즘 중 직선의 방정식을 기울기와 y절편을 이용해 구하는 방법과 매개변수 방정식을 이용해 나타내어 구하는 방법이 있습니다.
기울기와 y절편을 이용하는 방법은 초중고동안 비슷한 문제를 많이 풀며 익숙하지만 기울기가 무한, 즉 직선이 y축에 평행할 때 따로 조건을 분기해서 처리를 해야하는 번거로움이 있습니다.
또한 이 방법들은 직선의 방정식을 이용하는 방법들이기에 교점이 선분안에 존재하는지 확인해야합니다.
그래서 두 양 끝점을 종점으로 두는 벡터를 두고 그 벡터의 합을 이용해 직선을 표현하는 방식으로 교점을 구할 수 있습니다.
먼저 두 선분의 양 끝점 좌표를 각각 P1,y1/P2,y2/P3,y3/P4,y4라고 하겠습니다.
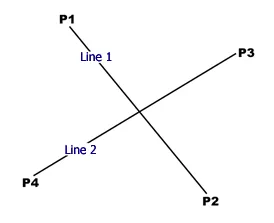
이 때 두 선분을 포함하는 직선의 방정식을 매개변수 t와 s를 사용하여 나타내면 다음과 같습니다.
P(t)=(1−t)P1+tP2 P(s)=(1−s)P3+sP4
이 때 선분을 나타내려면 t와 s는 0에서 1까지의 값을 가져야합니다.
두 선의 교점은 두 선이 모두 그 점을 지나므로 위 2개의 식을 아래와 같이 쓸 수 있습니다.
(1−t)P1+tP2=(1−s)P3+sP4
이 식을 x좌표와 y좌표로 분해해보면 다음과 같습니다.
x1+t(x2−x1)=x3+s(x4−x3)y1+t(y2−y1)=y3+s(y4−y3)
위 식을 t와 s에 대한 식으로 정리합니다.
(x2−x1)t−(x4−x3)s=x3−x1(y2−y1)t−(y4−y3)s=y3−y1
이 연립방정식을 행렬로 표현하면 다음과 같습니다.
(x2−x1y2−y1−(x4−x3)−(y4−y3))(ts)=(x3−x1y3−y1)
이제 이 식을 크레이머 공식을 이용해 t와 s에 대해 정리하면 다음값이 나옵니다.
t=(x1−x2)(y3−y4)−(y1−y2)(x3−x4)(x1−x3)(y3−y4)−(y1−y3)(x3−x4)
s=(y4−y3)(x2−x1)−(x4−x3)(y2−y1)(x2−x1)(y1−y3)−(y2−y1)(x1−x3)
크라메르 공식은 행렬식을 이용하여 연립방정식의 해를 구하는 공식으로 일반화된 공식은 다음과 같습니다.
Ax=B
위와 같은 조건일 때 x의 각 원소의 해는 다음과 같습니다.
xi=detAdetAi
이제 t와 s를 모두 구했으므로 처음 직선의 방정식에 대입해보면 아래와 같이 답을 구할 수 있습니다.
x=x1+t(x2−x1) y=y1+t(y2−y1)
이렇게 구했을때 구하는 도중 분모가 0이 되면 두 선은 평행하단 의미이고 분자,분모가 동시에 0이면 두 직선은 동일선상에 있습니다.
s와 t가 0에서 1사이가 아닌 경우 두 선분은 교차하지 않습니다.

